本节主要是介绍计算理论上的一些基本概念, 和一个最简单的计算模型, 即自动机模型. 自动机模型能解决的问题相当有限, 但是是图灵机模型的基础并且它足够简单, 因此以它作为一个入门是一个相当好的选择. 如果有学习过<算法导论>中的字符串匹配部分, 那么对这个概念应该并不陌生.
自动机模型和图灵机模型之间, 是下推自动机模型, 其功能强于自动机, 但弱于图灵机, 主要是程序语言理论中研究的核心模型, 我们暂且不研究程序语言理论, 因此也不介绍下推自动机.
计算问题
什么是计算机?
计算, 就是解决某个具体问题的算法, 得出相应的答案. 计算机就是能执行某个具体算法的机器. 即Computer就用来是Compute的机器. 此外, 讨论什么是机器, 对我们研究计算机科学毫无帮助, 你只需要知道, 计算机就是用来执行算法的机器. 我们要做的就是, 用最简单的理论模型, 最大程度的抽象化我们现有的计算机.
语言
定义 语言
一个字母表(alphabet)是一个非空有限集合, 该集合中的元素称为符号(symbol).
一个字母表$\Sigma$上的语言(language)是$\Sigma$中的元素构成的有限序列(称为串, 即string)的集合.
例如字母表$\Sigma=\{0,1\}$, 则我们可以定义一个$\Sigma$上的语言$L=\{x_1x_2\cdots x_n|\text{如果}x_i= 0,则x_{i+1}= 0\}$, 则该语言为
$$
L=\{\varepsilon, 0,1,10,11,100,110,111,\cdots\}
$$
即所有的$1$都出现在任何$0$之前的串. 其中, $\varepsilon$表示空串, 即长度为$0$的串.
这里要注意的是
- 我们说”序列”就要考虑顺序, 即$001$和$100$是不同的串.
- 串可以是空串, 即长度为$0$的串, 空串通常记作$\varepsilon$.
我们也可用更加形式化的描述来定义语言.
定义 语言
设$\Sigma$是一个字母表, $\Sigma^0=\{\varepsilon\}$表示空串的集合, $\Sigma^n=\Sigma\times \Sigma\times\cdots\times \Sigma$为$n$个$\Sigma$的直积. 则$\Sigma$上的一个语言定义为$\Sigma^\ast=\bigcup\limits_{i\in\mathbb{N}}\Sigma^i$的子集.
这里要注意的是$\Sigma^0$不是空集, 而是含有一个特殊的元素$\varepsilon$.
语言这个词可以说是一个相当糟糕的术语, 我们在这里不对这个术语本身进行过多的讨论, 但我们举例说明语言有多强大. 我们举一个有意义的例子.
例如, 一个语言可以用来表示所有的有向无环图, 我们试图用字母表$\Sigma=\{0,1\}$上的语言来对图进行编码. 首先我们需要表示图$G=(V,E)$中的$V$, 我们约定$\dagger$之前的部分表示图中每个点的名称的长度$v$, 而$\dagger$之后依次的每个长度为$v$的连续子串表示图所有点的名称. 在所有的名称后, 我们用另一个$\dagger$作为分割, 其后依次的每个长度为$2v$子串表示一条有向边. 所有的有向边后以$\ddagger$结束.
例如图
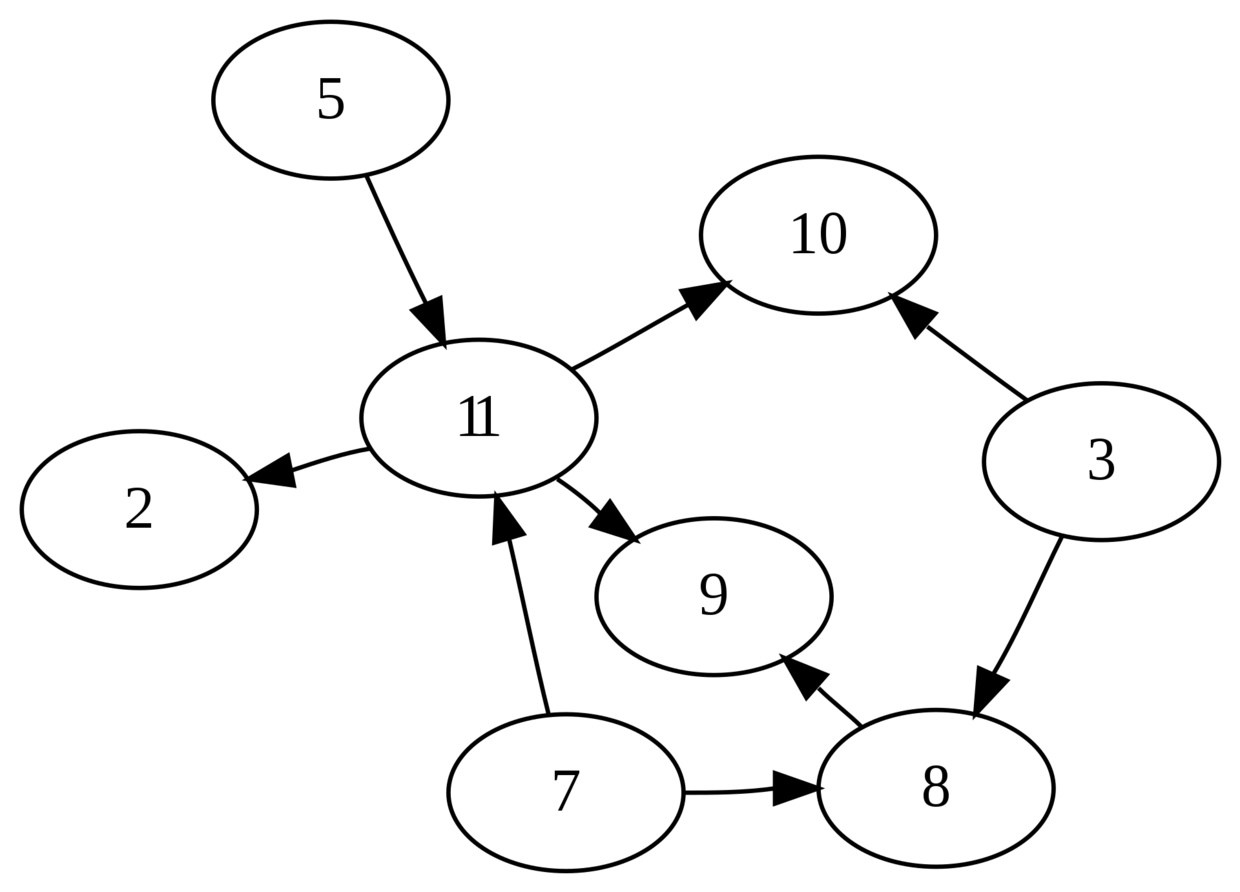
可以被表示为
$$
100\dagger0010\cdot0011\cdot0101\cdot0111\cdot1000\cdot1001\cdot1010\cdot1010\cdot1011\dagger\\0011\to1000\cdot0011\to1010\cdot0011\to1010\cdot0101\to1011\cdot\\0111\to1000\cdot0111\to1011\cdot 1000\to1001\cdot1011\to0010\cdot\\10011\to1010\ddagger
$$
在上述编码中, 作如下替换
$$
0\to01,1\to10,\dagger\to00,\ddagger\to11,\cdot\to\varepsilon
$$
即为该有向图的在该语言中的编码. 所有的有向无环图构成的语言, 即所有的有向无环图按照上述编码构成的语言. 值得一提的是, 上述语言对有向图的编码并不是双射, 但是我们可以增适当的限制使得该语言对有向图的编码成为双射.
按照类似的方式, 我们可以用语言表示, 所有的合取范式\无环布尔电路\树等. 大多数情况下, 我们不讨论具体的编码方式, 而是直接讨论语言, 如”所有的合取范式构成的语言”.
判定问题
计算理论中最简单的问题, 就是判定问题, 即只能用$\text{YES},\text{NO}$回答的问题. 这类问题非常普遍, 例如问某个有向图是不是有向无环图, 那么这个问题的算法, 实际上是建立了一个映射. 如果用$L_{G}$表示所有的有向图构成的语言, 并用$0,1$分别表示$\text{YES},\text{NO}$, 那么这个问题实际上就是建立了一个映射$f:\{0,1\}^\ast\to \{0,1\}$, 且$f(x)=1$当且仅当$x\in L_G$. 而解决这个问题算法就是能够计算函数$f$的算法.
不难得出, 每一个语言都对应一个判定问题, 因此我们不再区分语言和判定问题, 我们可以直接说判定问题$L_G$, 即判定一个有向图是否为有向无环图的问题. 此后的绝大多数情况, 我们关心的问题都是判定问题.
有的读者会问, 为什么我们要如此关注判定问题? 因为在未接触到这方面理论的人的直观思维中, 判定问题是一类非常弱的问题, 弱到连自然数的加法都无法计算. 确实如此, 但是判定问题和非判定问题之间存在天然的关系, 每一个非判定问题都可以转换为判定问题. 例如, 计算问题$f:(x,y)\mapsto x+y$可以转换为判定问题$g:\{(x,y,z)|x,y,z\in\mathbb{Z}_+\}\to\{0,1\}$, 其中$g(x,y,z)=1$当且仅当$x+y=z$, 即判定$z$是否为$x$和$y$的和的问题. 而且两者的复杂度之间存在深刻的关系, 我们将在之后的章节中具体介绍.
自动机模型
有限状态机
定义 有限状态机 (finite state machine)
一个有限状态机是一个五元组$(Q,\Sigma,\delta,q_0,F)$, 其中
- $Q$是一个有限集, 称为状态集
- $\Sigma$是一个有限集, 称为字母表
- $\delta:Q\times\Sigma \to Q$称为转移函数
- $q_0\in Q$是起始状态
- $F\subseteq Q$是接受状态集
有限状态机也称为自动机(automaton).
自动机不是什么复杂的东西, 一个自动机可以用一张类似于这样的图表示:
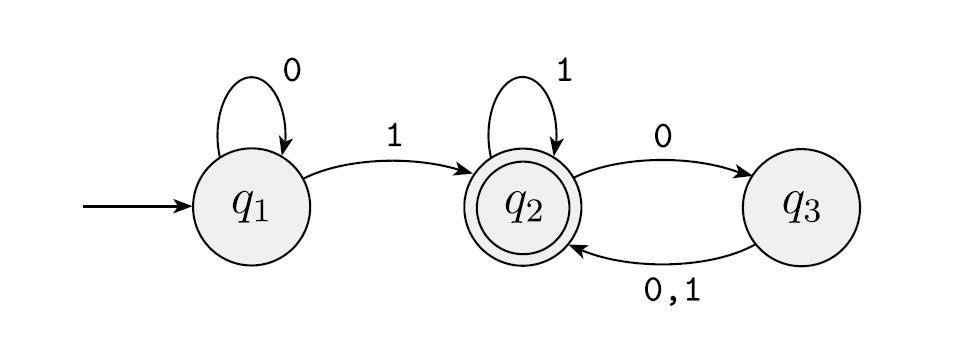
其中:
圆圈表示状态
- 有一条没有起点的箭头指向的状态为起始状态
- 双圈表示的状态是接受状态
带符号集的箭头表示转移函数中的一组映射
例如$q_2\overset{0,1}{\longrightarrow}q_3$表示映射$(q_2,0)\mapsto q_3$和$(q_2,1)\mapsto q_3$两条映射
当有限自状态机处于某个状态的时候, 读取到相应的符号, 有限状态机会根据转移函数跳转到下一状态. 例如上图中, 当有限状态机处于$q_1$状态时, 如果读到的下一符号为$0$, 根据转移函数$(q_1,0)\mapsto q_1$, 则在读取该符号后, 有限状态集仍会处于$q_1$状态
注意:
- 有限状态机(finite state machine)也可以称为自动机(automaton), 但不能称为”有限自动机”.
- 我们说”自动机”就是指”有限状态机”, 而不是”有限状态机””下推自动机””非确定自动机”等一系列计算模型的统称.
复杂度类REG
现在我们要讨论一类相当简单的语言, 和由它们构成的复杂度类REG.
从上面有关于自动机的描述, 我们可以看到, 当自动机$M=(Q,\Sigma,\delta,q_0,F)$处于起始状态$q_0$时, 我们输入一个$\Sigma$上的串$x\in\Sigma^\ast$, $M$会依次读取串$x$上的符号, 并根据状态机作相应的状态转换. 当整个串$x$读取完毕后, $M$可能处于某个接受状态$q\in F$, 也可能处于某个非接受状态$q^\prime\notin F$. 如果一个串$x\in \Sigma^\ast$使$M$按照上述运行方式运行后, 处于某个接受状态, 就记$M(x)=1$并称$M$接受串$x$, 否则记$M(x)0=$并称$M$拒绝串$x$.
这里要注意拒绝状态有两种情况. 一种是在输入结束后, 自动机确实处于某个非接受状态. 另一种是, 在输入的过程中, 某一部计算根据状态和输入符号, 转移函数中并没有一条映射指出这种情况下机器应该转移到哪个状态. 即, 计算提前结束了.
根据这一点, 我们可以发现, 自动机$M$根据上述运行的方式, 可以表示一个映射$f: \Sigma^\ast\to\{0,1\}$满足$f(x)=1$当且仅当$M(x)=1$. 如果一个语言$L$和一个自动机$M$满足$x\in L$当且仅当$M(x)=1$我们就说$M$识别(recognize)$L$或判定(decide). 为了统一我们有关判定的问题的叙述, 我们总是使用”判定”.
注意: 自动机是按照输入和转移函数按部就班地执行, 输入串中每一个符号都会让自动机执行一步, 且只会执行一步, 因此自动机总是在输入结束的时候停机, 因此不会出现不停机的情况. 在这样的限制下识别和判定是等价的, 但是对于其他的计算模型来说, 这两个概念并不等价.
现在我们定义一类判定问题(不要忘了一个语言对应一个判定问题, 判定问题的集合就是语言的集合)
$$
\textsf{REG}=\{L|\exists\text{自动机}M: x\in L\iff M(x)\}
$$
即REG表示那些能够被一台自动机识别的语言.
例: $L=\{所有包含”001”串\}\in \textsf{REG}$
我们可以构造一台识别它的自动机来说明这一点
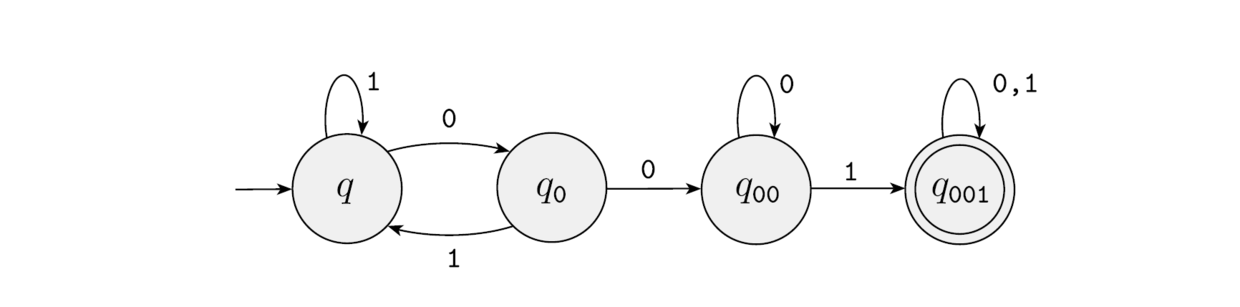
自动机作为计算机
自动机可以被视为一台计算机, 但是是一台功能相当弱的计算机. 抽象能力比较强的读者可以发现, 自动机没有任何类似于内存的结构, 所有需要存储中间值的才能完成的判定问题都不能被自动机完成. 我们称一个计算模型能够解决问题的能力称为计算能力, 如果考虑的是判定问题, 那么它表示的就该模型能够判定的语言的集合的一些特征(如和其他模型能够判定的语言的).
正则语言与自动机
正则语言
现在我们语言的三种运算方式, 它们的运算结果仍是一个语言. 设$L_1$与$L_2$均为语言, 定义它们之间的三种运算:
$$
L_1\circ L_2 = \{x_1x_2|x_1\in L_1, x_2\in L_2\}
$$
即$L_1\circ L_2$是所有$L_1$中的串与$L_2$中的串拼接构成的串的集合, 在不产生歧义的时候, 这个圈可以不写. 根据concatenation的翻译, 我们可以称该运算为”串联”.
$$
L_1\cup L_2 = \{x|x\in L_1 或 x\in L_2\}
$$
它所表示的意义和集合的并集一样.
而$L_1^\ast$表示的是由$L_1$中的任意串重复任意次(如果重复$0$次就得到$\varepsilon$)所得到的所有的串构成的集合. 例如$L_1=\{00, 01\}$, 那么$\varepsilon,00,01,0000,0101,000000,010101$等都是$L_1^\ast$的元素. 如果读者更倾向于形式化的定义, 那么$L_1^\ast$可以定义为
$$
L^0=\{\varepsilon\}, \quad L^n=\{x^n|x\in L\} \\
L^\ast= \bigcup_{i\in\mathbb{N}} L^i
$$
这三种运算称为正则运算, 我们不过度纠结运算的优先级问题, 并总是在需要的时候用括号表示运算的顺序.
现在我们来定义正则语言(regular language), 它包括一类最基本的语言, 和这类最基本的语言按照上述三种方式做运算产生的语言.
定义 正则语言
一个语言$L$是正则语言, 如果它满足以下命题之一
- $L=\{a\}$, 其中$a$是某个字母表$\Sigma$上的符号;
- $L=\{\varepsilon\}$;
- $L=\emptyset$;
- $L=L_1\cup L_2$, 其中$L_1$和$L_2$均为正则语言;
- $L=L_1\circ L_2$, 其中$L_1$和$L_2$均为正则语言;
- $L=L_1^\ast$, 其中$L_1$为正则语言;
要注意的是, 4.5.6.表示的运算中, 空集也可以参与, 并且有:
- 空集与任何语言作$\circ$或$\cup$运算得到的都是空集
- $\emptyset^\ast=\{\varepsilon\}$
这两点实际上也可以通过这些运算的定义得出.
如果是初次接触正则语言可能会觉得有些奇怪, 但是我们在学习正则表达式并了解自动机与正则语言的关系后, 这个概念会变得更加清晰.
从正则语言的定义种可以得到, 一个仅包含有限个串的语言总是一个正则语言, 因为它可以写成它的所有单个串构成的语言的$\cup$. 而每个单个串构成的语言又可以看作是仅有一个长度为1的串构成的语言的并联.
正则表达式
注意! 我们这里介绍的并不是用于在Linux系统中查询的正则表达式, 尽管我们介绍的正则表达式和它的功能一致. 但我们也会对Linux系统中的正则表达式某些符号的具体意思做出解释.
正则表达式(regular expression)是用来描述一个正则语言的, 它由字母表种的符号, $\cup$运算符, $\circ$运算符, $^\ast$运算符还有括号组成. 我们可以用这些符号连同括号的组合来表示一个正则语言, 同样的, 这里的$\circ$在不产生歧义的情况下也可以略去不写.
例如, 正则表达式$R = (0\circ(0\cup 1))^\ast$, 表示语言
$$
L=\{\varepsilon, 00, 01, 0000, 0100, 0101, \cdots\}
$$
即所有长度为偶数且$1$只出现在从左至右第偶数位的串. 它的原理很简单, 它由长度为2单元$0\circ (0\cup 1)$重复任意次组成, 而在一以个单元种, 第一位必须是0, 第二位可以是1或0. 实际上这个语言确实是正则语言, 令$L_0=\{0\}, L_1=\{1\}$, 那么有
$$
L= (L_0\circ (L_0\cup L_1))^\ast
$$
显然复合正则语言的定义.
我们现在来定义正则表达式, 并用一些例子在说明它是如何运作的.
定义 正则表达式
一个表达式$R$为正则表达式, 如果它是以下几种表达式之一
- $a$, 其中$a$是字母表$\Sigma$中的一个元素;
- $\varepsilon$;
- $\emptyset$;
- $(R_1\cup R_2)$, 其中$R_1$和$R_2$是正则表达式
- $(R_1\circ R_2)$, 其中$R_1$和$R_2$是正则表达式
- $(R_1^\ast)$, 其中$R_1$是正则表达式
同时这里也要注意和空集的运算, 与正则语言类似, 这里不再赘述.
可以看出, 正则语言和正则表达式非常相似. 注意有时候, 我们会简化正则表达式的写法, 让整个串充当一个字母的角色, 并且可以用或($|$)连接一些串, 同时出现可选串$[]$. 例如
$$
R= (10 | 01) [00] 1
$$
表示语言
$$
L={101,011,10001,01001}
$$
它的原理也非常简单, 每个串都是一些仅有字母表中一个符号构成的语言的串联, 而或($|$)表示的就是$\cup$, 而$[x]$表示的是$x|\varepsilon$. 用这种方式表达的正则表达式, 就是我们常用于查询的正则表达式.
而如果或($|$)连接的是一些长度为1的串, 我们也更习惯将它表示为这些串的符号的集合, 例如$(a|b|c)^\ast$可以表示为$\{a,b,c\}^\ast$, 如果这个集合就是字母表$\Sigma$, 我们还可以写作$\Sigma^\ast$. 同时, 如果我们希望重复一个串$x$大于等于$1$次也可以用$x^+$来表示, 即$x^+=x \circ (x^\ast)$.
例子 设$\Sigma=\{0,1\}$
- $0^\ast 10^\ast=\{w|w恰好有一个1\}$
- $(\Sigma\Sigma\Sigma)^\ast=\{w|w的长度正好是3的倍数\}$
- $2333(3^\ast)=\{w|w是由2333开头且在之后是任意长度的纯3串\}$
其中3.中表示的正则表达式有助于屏蔽弹幕中那些过长的类$233$串, 例如$2333333333333333333333$.
注意: 我们始终没有证明正则语言和正则表达式的对等性, 即一个正则表达式表示一个正则语言, 一个正则语言总可以用一个正则表达式表示. 我们不打算证明这一点, 因为我们认为读者的直觉能够察觉这一点, 如果喜欢学习严格的证明, 还是请阅读教材或论文.
定理1
一个语言$L$是正则语言, 当且仅当它能够被表示成某个正则表达式$R$.
非确定自动机
非确定性
非确定性(nondeterminism)是不是非确定自动机独有的, 我们还会在其他的计算模型中遇到非确定性, 因此我们决定先介绍非确定性, 再介绍非确定自动机.
在自动机模型中, 一个自动机在接受相同的输入时, 总是执行相同的计算步骤, 并总是得到相同的结果, 这样的计算方式称为确定的(deterministic). 即, 计算步骤与时间无关(如果我们将从宇宙大爆炸到目前为止的时间视作一个隐藏的参数的话/如果读者知道实时系统的定义, 那么对这个描述应该不会感到突兀). 这可能有点决定论的味道, 但也是一种理解方式. 反之, 非确定性, 就是, 一次具体的计算过程, 与时间有关. 或者, 我们可以更加直观地说, 一台具有非确定性的计算机, 在接受相同输入时, 计算步骤和结果可能有所不同.
非确定自动机
自动机具有确定性是因为自动机处在任意状态时, 对于某个具体的输入, 根据转移函数, 改机器仅能转移到至多一个状态, 即转移的结果是唯一的. 如果我们修改这一条定义, 将转移的方式改为不确定的, 那么我们就得到非确定自动机(nondeterministic automaton).
为了避免读者对于陌生数学符号的恐惧, 我们解释一下超集. 有限集的超集非常容易理解, 一个有限集$S$的超集, 是它的所有子集的集合, 记作$\mathcal{P}(S)$. 例如$S=\{a,b,c\}$, 那么它一共有8个子集
$$
\emptyset,\{a\},\{b\},\{c\},\{ab\},\{ac\},\{bc\},\{abc\}
$$
其超集就是以上8个集合组成的集族(一般我们称集合的集合为集族, 也可简称为族).
定义 非确定自动机
一个非确定自动机是一个五元组$(Q,\Sigma_{\varepsilon},\delta,q_0,F)$, 其中
- $Q$是一个有限集, 称为状态集
- $\Sigma_{\varepsilon}$是一个有限集, 是字母表和空串$\varepsilon$的并集.
- $\delta:Q\times\Sigma_\varepsilon \to \mathcal{P}(Q)$称为转移函数
- $q_0\in Q$是起始状态
- $F\subseteq Q$是接受状态集
这里与自动机相比, 唯一不同的一点在于转移函数, 非确定自动机的转移函数的上域(codomain)(注意不是值域!)变为了状态集$Q$的超集$\mathcal{P}(Q)$. 除此之外, 非确定自动机的转移函数还能接受输入$\varepsilon$, 即在不接受任何输入的时候也可能随机发生转移. 回想一下, 自动机在处于某个状态时, 接受某个符号会转移到一个唯一确定的状态, 而处于某个状态的非确定自动机, 接受某个符号的输入, 则会有一些状态构成的集合作为”候选”状态, 非确定自动机会随机地从这些状态中选择一个进行转移.
如果我们将非确定自动机的每一次转移视作它产生了几个并行的计算分支, 那么我们由如下图所示的描述
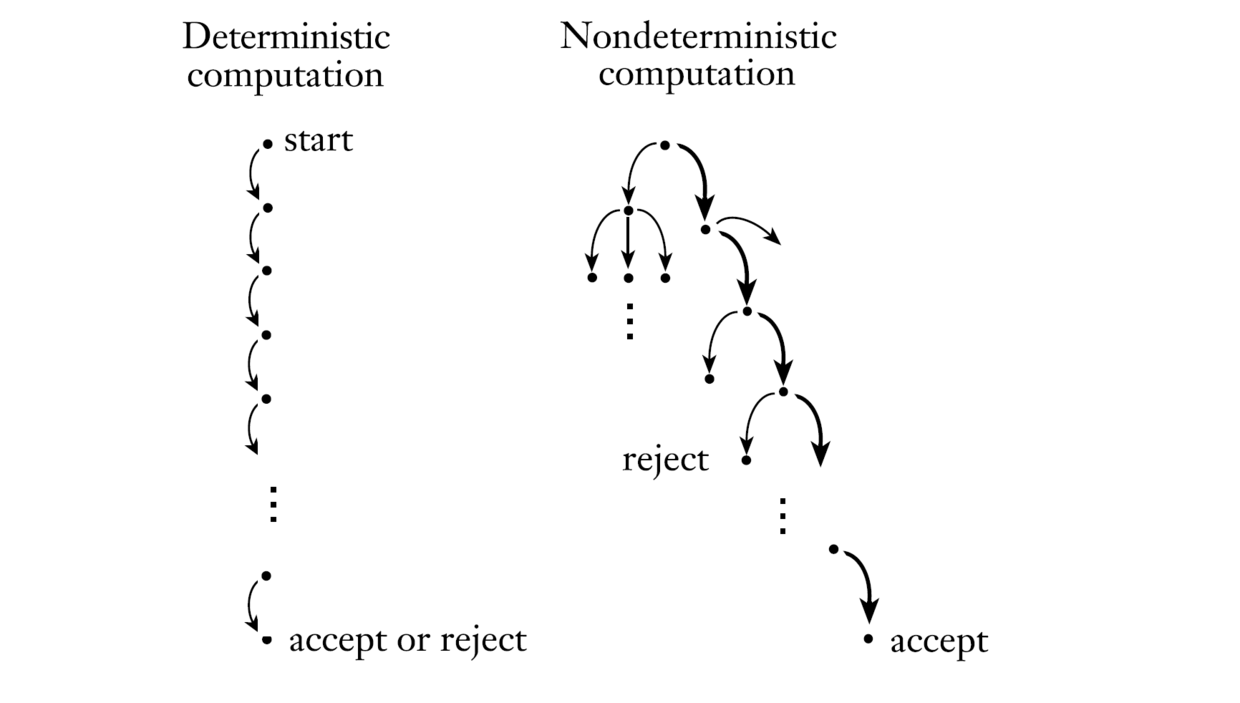
其中左图为自动机的计算步骤, 其每一步计算都是仅产生一个计算分支, 而整个计算过程由一个计算分支过程, 自动机是否决定某个串, 取决于这个唯一的计算分支是否在串的输入结束后处于接受状态. 类似的, 我们通过这一点将接受的概念推广到非确定自动机上.
非确定自动机每一步都会产生多个计算分支, 而整个计算过程的计算分支可能会非常复杂. 非确定自动机的整个计算过程可以用一个深度和输入长度加1相等的树来表示, 其每个节点都是一个非确定自动机的状态, 而路径则是合法的转移. 通过这种方式, 我们可以知道, 每一条根到叶子的路径都是一条计算分支. 先在我们定义: 如果非确定自动机$N$在输入$x$时存在一条计算分支在输入结束后处于接受状态, 我们就说非确定自动机$N$接受输入$x$, 记作$N(x)=1$. 否则, 我们称非确定自动机$N$拒绝串$x$, 记作$N(x)=0$.
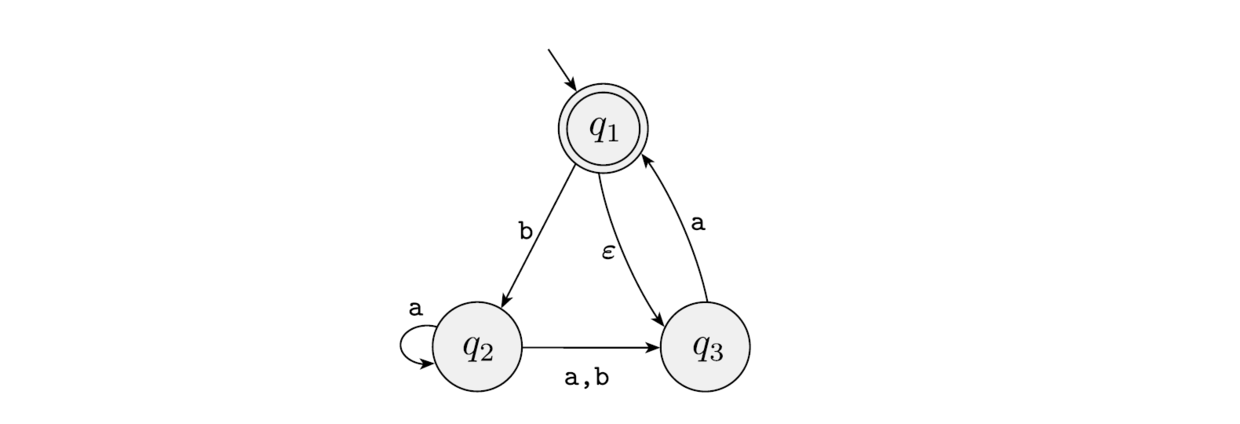
例如下面的非确定自动机, 处在$q_1$状态时, 可能会随机转移到$q_3$状态. 而当它处于$q_2$状态并收到输入$a$时, 可能转移到$q_2$或$q_3$状态. 当模拟其计算过程时, 可以计算通过将每一步机器可能处于的状态视作一个集合(我们称为合法状态集), 并在收到某个输入符号时, 计算每个合法状态集中的状态对应该符号根据转移函数得到的状态集合的并集. 例如下图中的非确定自动机根据输入$bc$
- 首先在起始状态时, 可能随机转移到状态$q_3$, 因此此时的合法状态集是$\{q_1,q_3\}$
- 在收到第一个输入$b$时, 状态$q_1$只能转移到$q_2$, 而状态$q_3$根据输入$b$无法转移, 因此这一步的合法状态集为$\{q_2\}$
- 在收到第二个输入$c$时, 状态$q_2$无法转移, 因此这一步的合法状态集为$\emptyset$.
因此该非确定自动机应该是拒绝串$bc$.
如果熟悉并行计算, 那么非确定自动机的计算步骤可以理解为”并行的”, 即每一条计算分支相当于被非确定自动机并行的执行了. 需要注意的是, 计算分支数很可能是无限多的, 这样的机器在现实世界中也太可能被制造出, 但可以通过算法模拟.
非确定自动机的计算能力
从自动机与非确定自动机的定义可以看出, 自动机是非确定自动机中很特殊的一类机器, 相当于是机器处于任意状态时, 收到任意输入符号, 仅能转移到至多一个状态的非确定自动机.
现在我们通过建立一台指定任意非确定自动机$N$计算能力相同的自动机$M$, 来说明, 自动机和非确定自动的计算能力是相同的. 即
定理2
设$L$为语言. 存在一台自动机$M$判定$L$, 当且仅当存在一台非确定自动机$N$判定$L$.
回想一下我们”合法状态集”, 非确定自动机$N$处在某一步计算时, 在接受另一个输入, 可以视作从一个合法状态集转移到了一个另一个合法状态集, 而一个输入是否被接受, 取决于非确定自动机在该输入下最后一步计算对应的合法状态集中是否有接受状态, 因此我们通过这一点, 将一台非确定自动机$N(Q, \Sigma_\varepsilon,\delta, q_0,F)$, 变为一台自动机$M$.
- 由于每一步计算都视为合法状态集到合法状态集的转换, 因此, $M$中的状态集应该是$Q$的超集, 即$\mathcal{P}(Q)$.
- 由于自动机不能发生随机转移, 因此, $\varepsilon$不能参与转移, 即自动机的第二个参数退化为$\Sigma$.
- 转移函数$\delta^\prime$肯定是一个$\mathcal{P}(Q)\times \Sigma \to \mathcal{P}(Q)$的集合, 显然这个转移是确定的, 因为每一个$\mathcal{P}(Q)$中的元素都能够被$M$的一个状态表示.
- $M$的起始$q_0^\prime$状态是$q_0$及$q_0$能随机转移到的那些状态构成的集合.
- $M$的接受状态集是所有含有$F$中任意元素的集合的集合.
通过这样的转换, 我们容易证明, $M(x)=1$当且仅当$N(x)=1$.
正则语言与非确定自动机
令人惊奇的是, 任何一个正则语言, 都能被一台非确定自动机判定, 而任何一台非确定自动机判定的语言都是正则语言. 我们不打算证明这一点(因为教材上的证明非常详细), 但是会介绍一下如何将一个正则语言转换为判定它的非确定自动机.
定理
一个语言$L$是正则语言, 当且仅当存在一台非确定自动机$N$可以判定它.
广义非确定自动机**. 广义非确定自动机是非确定自动机的推广版本, 它的定义和非确定自动机类似. 唯一不同的一点在于, 其转移函数$\delta$表示的映射是$Q\times \Pi \to \mathcal{P}(Q)$, 其中$\Pi$表示所有正则表达式的集合. 用通俗的语言来讲, 它的状态集图上箭头的标号可以不仅是语言中的某个符号, 而是可以是整个正则表达式. 我们已经很清楚的知道, 每个正则表达式确实就是表示了某个正则语言, 因此, 广义非确定自动机的转移是在读取一个串后进行的.
现在, 我们根据一个正则表达式可以做出最原始的广义非确定自动机, 例如对正则表达式$R$, 我们可以作出状态机图$q_0\overset{R}{\to}q_1$. 其中$q_0$是其实状态, $\{q_1\}$是接受状态集. 我们考虑正则语言的三种操作, 将它表示转移函数中的正则表达式仅有最基础的三种正则表达式(即$\varepsilon$, $\emptyset$, 单个符号$a$)的广义非确定自动机(这其中$\emptyset$标注的转移函数又可以略去不写).
我们的任务很简单: 逐步将判定$R$的广义非确定自动机$G$化为非确定自动机$N$. 首先, 如果$R$是三种最平凡的正则表达式($\emptyset$, 仅含一个单个符号的正则表达式, 正则表达式$\varepsilon$)中的一种, 那么$G$就已经是非确定自动机了. 如果$R$是由两个正则表达式$R_1,R_2$按照三种运算($\cup$, $\circ$, $\ast$)组成的, 那么我们按照以下方式处理.
- $R=R_1\cup R_2$
只需要将下图中的作图转换为右图即可. 如果左图中的$q_1$是接受状态, 则右图中的$q_{11},q_{12}$均为接受状态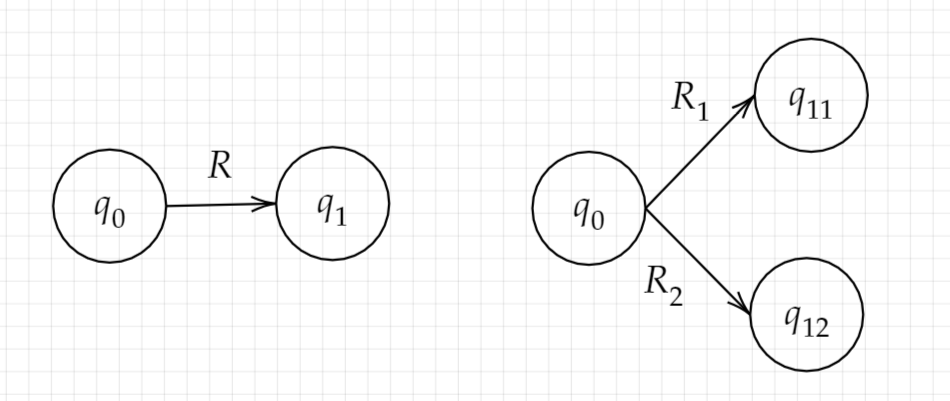
- $R=R_1\circ R_2$
只需将下图的左图转换为右图即可. 如果左图中的$q_1$是接受状态, 则右图中的$q_{12}$是接受状态.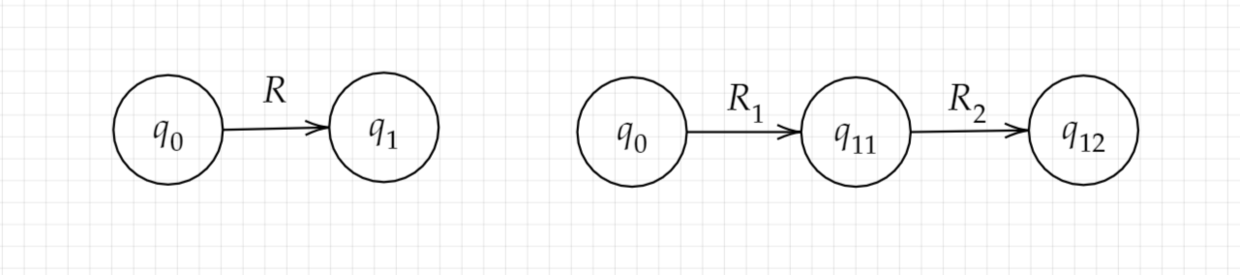
- $R=R_1^\ast$
只需将下图中的作图转换为右图即可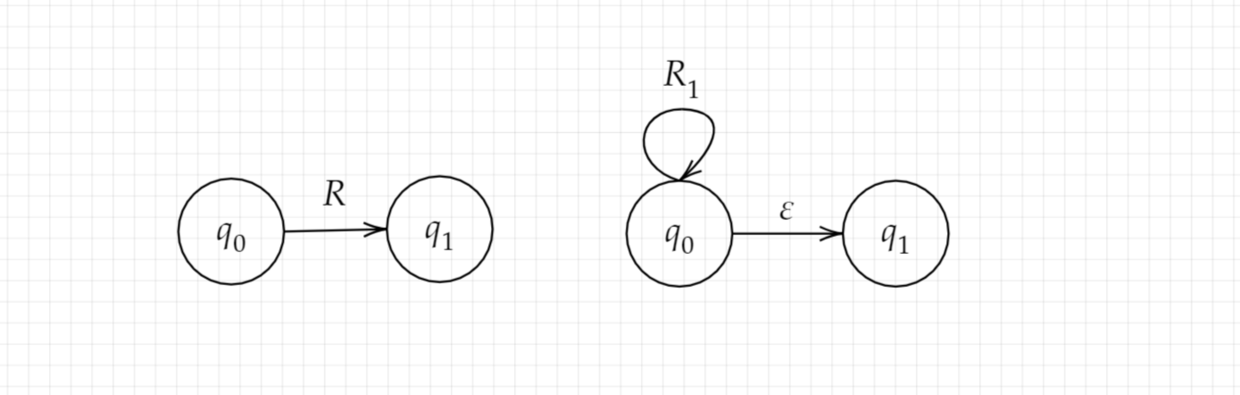
通过递归地进行以上三种操作, 任何一个正则表达式都可以在有限步骤内转为为一台判定它的非确定自动机, 因此我们证明了定理3. 同时, 根据定理1, 我们有
定理4
语言$L$是正则语言, 当且仅当存在一台非确定自动机$N$, 满足$x\in L\iff N(x)=1$.
正则语言与自动机
根据定理2, 一台非确定自动机总能够转换为一台计算能力和它相同的非确定自动机, 因此, 根据定理4我们有
定理5
语言$L$是正则语言, 当且仅当存在一台自动机$M$, 满足$x\in L\iff M(x)=1$.
泵引理
我们介绍的泵引理(pumping lemma)是一个用于判断一个语言是否为正则语言的引理. 泵引理给出了一个语言是正则语言的必要而非充分条件, 我们不证明该引理, 但是会对它做一些直观上的解释, 并且举例说名用它来证伪一个语言是正则语言.
引理6 泵引理
假设 ${ L\subseteq \Sigma ^{*}}$是正则语言, 存在字符串 ${ w\in L}$且$ { \left|w\right|\geq n}$, 则以下说法成立:
- ${ \left|xy\right|\leq n} $
- ${ \left|y\right|\geq 1}$
- ${ \forall k\geq 0:xy^{k}z\in L}$
习题
- 编写一个判定正则语言的程序$P_1:x\to \{0,1\}$, 程序的输入是一个正则表达式$R$和一个串$x$. 设正则表达式$R$表示的语言为$L$. $P_1(x)=1\iff x\in L$.