群论最基本的知识, 和一个有趣的例子.
运算
集合$G$上的二元运算是指函数
$$
\ast:G\times G\to G
$$
如果$a\ast b=b\ast a$则$\ast$交换律成立.
运算并不是什么特别的东西, 我们可以借助我们熟悉的函数的概念来理解它. 一个运算就是一个二元函数, 而且定义域和值域相同, 都是$G$, 即
$$
\ast: G\times G\to G
$$
群
带有运算$\ast$和特殊元$e$的集合称为群,如果满足:
- 结合律成立,对于任意$a,b,c\in G$有
$$
a\ast(b\ast c)=(a\ast b)\ast c
$$- 对所有$a\in G$有$e\ast a=a$
- 对于任意$a\in G$,存在$a^\prime\in G$有$a^\prime\ast a=e$
群也是一种很自然的定义, 在函数$\ast$定义域和值域的基础上, 再加上存在单位元和每个元素存在逆元的情况下, 就是群.
一种有意思的群就是魔方群. 对于一个魔方, 我们可以定义对魔方的多种操作. 将魔方按照任意一种顺序拧过后, 这些顺序组合就是一种操作. 所有的操作构成一个群. 现在我们一次来验证这些操作是否满足群的定义.
在验证之前, 我们需要对符号做一些说名, 所有的单步操作如图所示
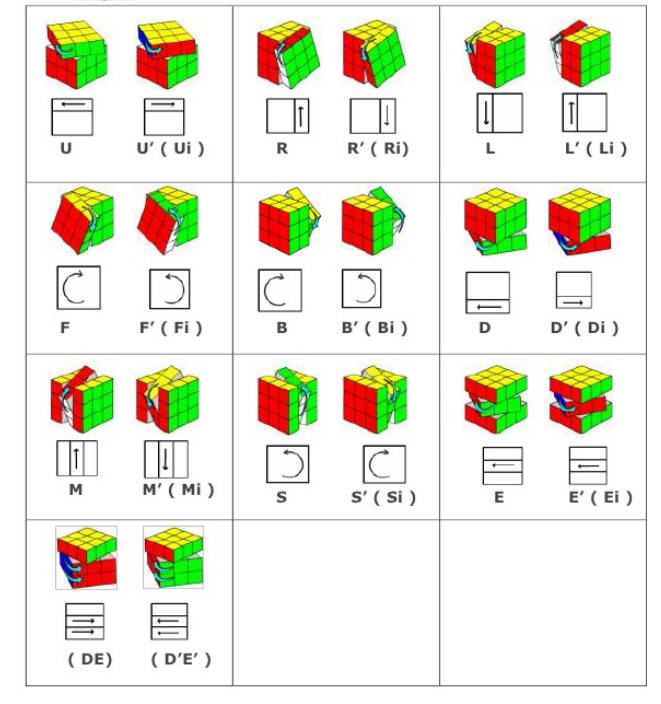
而操作可以是多步的, 我们用$P$来表示一个操作, 并可以将它表示为一系列基本(单步)操作的依次进行, 如$P=MFE^\prime$, 表示依次按照如图所示的$M$,$F$,$E^\prime$对魔方进行操作. 这种一次进行操作, 就是魔方群的运算.
结合律 我们可以把多步操作和并看作一步操作, 也就是加括号的操作. 也可以将一步操作, 写为多步操作, 也就是去括号. 这个加和去括号的操作都是任意的, 不会概念最终结果, 因此魔方操作具有结合律.
封闭性 显然, 任何两个操作的运算仍然是一个操作.
单位元 现在我们将没有任何操作也视作一个操作, 记作$I$, 那么对于任何$P$都有$PI=IP=P$, 即$E$就是这个群的单位元.
逆元 我们用$E_i$表示一个基本操作, 那么对于任何一个操作$P$都可以被分解为基本操作, 即$P=E_1 E_2\cdots E_n$, 现在我们要找$P$的逆操作$P^\prime$, 即$PP^\prime=I$. 显然, $I=E_1E_2\cdots E_i E_i^\prime E_{i-1}^\prime \cdots E_1^\prime$, 因此按照基本操作逆着来做一次, 总可以恢复魔方最初的样子, 因此对于任意$P=E_1 E_2\cdots E_n$有$P^\prime=E_i^\prime E_{i-1}^\prime \cdots E_1^\prime$使得$PP^\prime=P^\prime P=I$.
上述几个条件满足, 使得所有魔方操作构成一个群, 即魔方群. 上述描述不太严谨, 只是为了易于读者的理解而举的生活中常见的例子.
阿贝尔群
如果群$G$的运算满足交换律,即对于任意$a,b\in G$有$a\ast b = b\ast a$,则称$G$为阿贝尔群.
实际上, 阿贝尔群和非阿贝尔群我们应该都见过, 非阿贝尔群最典型的例子就是, 行列式非零的所有$n\times n$的实矩阵构成的矩阵乘法群, 请自行验证.
元素的阶
群$G$中元素$a$若对于某个$k\geq 1$有$a^k=1$,则这样的最小这指数$k$称为$a$的阶,如果这样的幂不存在,则称$a$有无限阶.
子群
如果$H\subseteq G$,且$H$满足群的公理,则称$H$为$G$的子群,记作$H\leq G$.
- 在不需要考虑$H\neq G$是否成立的时候也可以直接记作$H<G$
下面几个命题, 请根据群的定义自行证明:
- 群$G$的子集$H$是一个子群当且仅当$H$非空,且对任意$x,y\in H$有$xy^{-1}\in H$
- 群$G$的子集$H$是一个子群当且仅当$H$非空且在群$G$的运算下封闭,即对于任意$a,b\in H$有$ab\in H$.
- 若$H_i\leq G$,则$\bigcap_\limits{i\in I}H_i\leq G$
陪集
若$H<G$且$a\in H$,则左陪集定义为
$$
aH=\{ah|h\in H\}
$$
- 对于非阿贝尔群,左陪集和右陪集应该分别定义.
定理
设$H<G$且$a,b\in G$
- $aH=bH$当且仅当$b^{-1}a\in H$. 特别地,$aH=H$当且仅当$a\in H$.
- 若$aH\cap bH\neq\O$,则$aH=bH$
- 度所有$a\in G$有$|aH|=|bH|$
对2的批注:
- 这是由于同一子群的所有陪集构成了群的一个划分. 当然这是结论, 不是证明过程.
对3的批注:
- 即同一子群的所有陪集势相等.
- 这是由于将子群映射为陪集的函数$f:H\to aH, h\mapsto ah$为双射
注意:
- 诸如$aH$这样的记号还有$gHg^{-1},HK$等,它们的原理一样,我们可以放心使用
- 陪集之间要么相等,要么不相交,如上述定理的2.
拉格朗日定理定理
若$H$为有限群$G$的一个子群,则$|H|$是$|G|$的一个因子.
- 由陪集之间不相交且阶数相同显然可以得到这个结论
指标 (Index)
群$G$的子群$H$的陪集的个数称为$H$在$G$中的指数,记作$[G:H]$
- $推论$: $[G:H]=|G|/|H|$
- 若有限群$G$的阶是$m$,则对所有$a\in G$有$a^m=1_G$