本节介绍现代密码学中对安全的定义. 这些定义通常精巧又微妙, 是密码学入门的难点, 因此好好理解它们对于整个学习过程非常重要.
介绍
现代密码学是一套基于严格的公理系统的科学, 对于安全性有着严格的定义. 在现代密码学中, 密码方案的安全性不能再凭经验判断, 只有经过严格安全性证明的加密方案, 才具有安全性. 现代密码学中常提到的安全性, 是计算意义上的安全性, 在大量计算复杂性上的问题尚无答案的时代背景下, 密码算法的安全性通常是基于困难问题假设的安全性.
路线
我们将从密码算法的定义出发, 研究理论上完全的安全性, 然后转而介绍计算意义上的安全性定义.
公钥密码算法
对称密码方案非常容易刻画, 即存在两个人Alice与Bob, 他们想要相互私密地通讯, 但是Alice与Bob所使用传递消息的信道并不是一个安全的信道, 即窃听者Eve可以从信道中听到Alice与Bob之间传输的内容. 这个时候, Alice与Bob需要用加密的方式来保护他们传递的信息, 将消息明文(plaintext)$m$转换为密文(ciphertext)$c$再发送, 另一方拿到密文$c$后, 再解密出明文$m^\prime$. 我们现在先考虑对称密码的情形, 在对称密码中$m^\prime=m$始终成立且Alice与Bob都将要使用事先都协定好的一串信息$k$来对他们发送的消息进行处理, 也就是密钥. Alice与Bob之间的需求可以用下图描述:
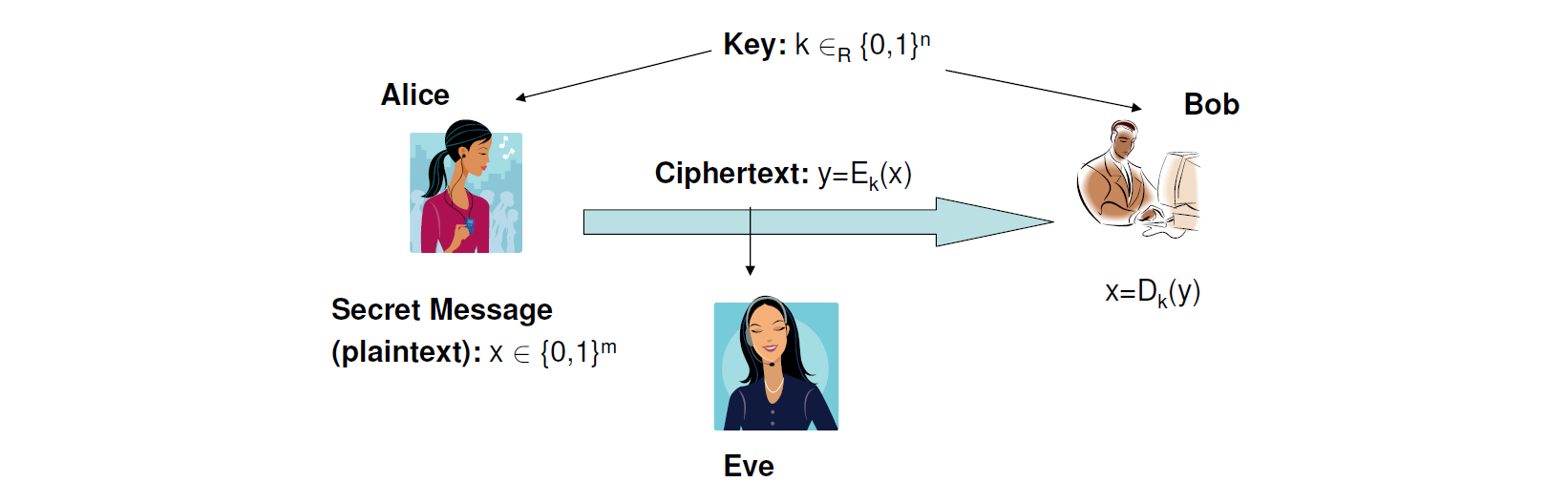
先在, 我们定义形式化定义一下公钥密码方案. 注意:
- 我们目前定义的加密方案还不是安全的加密方案, 因为我们还没有定义什么是安全性.
- 根据计算模型的不同, 密码方案的定义略有不同, 请根据实际情况处理. 如我们这里定义的公钥密码算法加密和解密过程都是在确定图灵机上执行的, 当然你也可以将这个模型换为概率图灵或至是量子图灵机来定义密码方案.
公钥密码方案
一个公钥密码方案是一个算法三元组$(\mathsf{KeyGen},\mathsf{Enc},\mathsf{Dec})$, 其中
- $\mathsf{KeyGen}(1^n)=k\in \mathcal K$是一个可以在$\mathbf{BPP}$内计算的函数
- $\mathsf{Enc}: \mathcal K\times\mathcal M\to\mathcal C$是一个可以在$\mathbf{BPP}$内计算的函数
- $\mathsf{Dec}:\mathcal K \times\mathcal C\to \mathcal M$是要给可以在$\mathbf{P}$内计算的函数
且满足对于任意$k\in \mathcal K, m\in\mathcal M$有$\mathsf{Dec}(k,\mathsf{Enc}(k,m))=m$.
我们真的不想一次性拿出这么多奇怪的符号, 但是他们真的都是必要的. 作者认为有必要从一开始就形式化地描述任何一个概念. 我们现在要做的就是解释清楚这些符号, 来为之后的定义铺好路.
在公钥密码算法的定义中, 我们定义了三个算法, 算法和函数有两点不同:
- 算法可以是非确定(nondeterministic)的, 即对于同样的输入, 可能每次计算的输出可能会不同. 确定(deterministic)函数在这一点上和函数是相同的.
- 说”算法”要考虑他的复杂度, 而说”函数”时则不用考虑这一点.
至于什么是复杂度类$\mathbf{BPP}$建议在参考计算复杂性中的”随机化计算“一节(强烈建议你参考这一章节, 因为这里的随机和你所了解的随机真的不一样, 我们将用”掷硬币”的方式产生随机数, 从而避免有关”决定论 v.s. 随机论”的讨论, 当然这一节还尚未写作, 建议你先参考相关读物). 我们来几个每一个算法, 和描述它的其他符号来解释定义的每一条.
- $\mathsf{KeyGen}$即密钥生成算法, 该算法会在收到平凡的输入$1^n$(表示$n$个$1$组成的字符串), 随机从密钥空间$\mathcal K$中选取一个密钥. 注意, 我们并没有说明是如何”随机”, 因为具体是如何随机(例如是不是均匀分布), 这一点是由算法本身来决定的.
- $\mathsf{Enc}$即加密方案, 该算法会在输入密钥$k$与明文$m$后, 得到明文$m$在密钥$k$下的密文$c$. 注意$\mathcal M$和$\mathcal C$分别表示明文空间和密文空间, 他们是所有合法的明文或密文的集合.
- $\mathsf{Dec}$即加密方案, 该算法会在输入密钥$k$与密文$c$后, 得到密文$c$在密钥$k$下解密得到的明文$m^\prime$.
接下来我们需要明白的问题是, 为什么我们要将密钥生成, 加密, 解密的复杂度都限制在(概率)多项式时间内. 实际上为了安全起见, 我们可以将加密和解密算法都设计得非常复杂, 这样一来要破解加密方案就会变得非常难, 但是, 这样的坏处是加密算法将失去可行性. 例如一个加密和解密的复杂度都是$2^{|x|}$的算法, 那么, 假设算法每秒被执行$10^{10}$步, 加密和解密一个200比特的串都将用掉多余$1.6069\times10^{50}$秒, 这超过的宇宙的总寿命. 我们决定不在此探讨多项式时间作为可行的标准是否合适.
在定义中, 我们最后要求”对于任意$k\in \mathcal K, m\in\mathcal M$有$\mathsf{Dec}(k,\mathsf{Enc}(k,m))=m$”实际上就是说, 当加密方和解密方使用相同的密钥时, 对于任意消息, 解密方解密加密方给出的密文$c$, 要能够正确得出加密方最先加密的消息$m$.
信息论意义上的安全性
在定义公钥密码方案的时候, 我们似乎忘了一个最重要的东西, 那就是安全性. 我们缺乏对安全性的描述, 也就缺乏了加密方案安全性的保障, 密码算法随之也就失去意义. 例如, 一个密码方案, 加密后的密文即使在窃听者没有密钥的情况下也能很快从密文中恢复出明文, 那么这个密码方案就毫无意义.
我们首先来定义一种安全性, 该定义来源于香农的研究成果. 该定义中的安全性称为信息论意义上的安全, 也称绝对的安全性.
信息论意义上的安全性
设加密方案中密钥空间为$\mathcal K$, 明文空间为$\mathcal M$, 密文空间为$\mathcal C$, 对于任意$\mathcal M$上的消息分布, 任意密钥$k\in \mathcal K$, 任意消息$ m\in \mathcal M $和任意密文$c\in\mathcal C$满足$\Pr[C=c]>0$都有
$$
\Pr[M=m|C=c]=\Pr[M=m]
$$
这到底在说什么? 这个定义的直观解释依赖于条件概率的直观解释: 即任意的攻击在对密文毫无之情的情况下猜测消息$M$为$m$的概率, 等同于攻击者知道密文$C=c$的情况下猜测被加密的消息为$m$的概率——即密文没有提供任何额外的信息. 这就好比是一个敌手Eve想要猜测Alice与Bob之间发送的消息, 她在知道密文$c$和不知道任何密文的情况下猜测消息是$m$的概率相同——即知道了密文也和瞎猜一样.
具有这个定义下安全性的密码方案, 将具备完美的安全性, 只可惜香农证明了, 如果要达到这样的安全性, 密钥的长度至少要和被加密的消息一样长——这将使得加密方案变得非常不实用. 因此, 我们提出了一种折衷的方式, 即不需要让Eve对密文的信息永远都一无所知, 而是只需要让Eve在指定时间内以小于指定概率的破译出密文中的信息即可. 更加概括地讲, 就是要让密码方案对于计算能力受限的所有敌手来说是安全的. 我们采用的定义就是密码学中著名的$(t,\epsilon)$-安全的定义.
计算意义上的安全性
在叙述这个定义之前, 我们先对敌手做一个概括, 实际上我们的敌手来破解加密方案, 也就是使用一个算法来破解, 因此我们将所有的敌手都看作是算法, 并记作$\mathcal A$. 我们限制敌手的能力, 就是限制抽象为算法的敌手所使用的计算资源, 到目前为止我们都讨论的是和破解时间有关, 因此, 我们需要限制任意抽象为算法的敌手$\mathcal A$执行的时间.
根据该限制, 我们介绍一种新的安全性, 即$(t,\varepsilon)$-安全性. 我们说一个加密方案是$(t,\varepsilon)$安全的, 即是说任何在$t$时间内运行的概率性算法, 不能以高于$\varepsilon$的概率来破解这个算法. 当然, 这个定义仅在$t$较大和$\varepsilon$较小的才有意义. 接下来, 我们将用安全参数$\kappa$将上述定义形式化. 安全参数, 即同一套加密方案可以选择的参数, 加密和解密的复杂度以及安全性的参数都依赖于这个参数. 对于常见的密码算法来说, 这个参数可以认为是密钥的长度, 一般记作$n$.
一般来说, 我们认为加密和解密在多项式时间内完成是可以接受的, 那么破解算法就不能以这个时间完成, 因此我们要求, 任何破解算法在概率多项式时间内不能以多项式分之一的概率破解该算法. 否则, 根据$\mathbf{BPP}$算法的归约, 我们就可以构造一个概率多项式时间内的算法以大于$2/3$的破解密码. “不能以多项式分之一”是一个冗长的叙述, 因此我们给所有满足的函数启一个名字, 即可忽略小, 我们用$\mathsf{negl}(\cdot)$来表示一个可忽略小的函数, 现在我们给出形式化的定义.
可忽略小函数
设一个函数$f:\mathbb R_+\to \mathbb R_+$满足, 存在$N>0$使得当对于任意$c>0$和$n>N$有$f(n)<\frac{1}{n^c}$, 则称函数$f$是可忽略小的, 记作$f(n)=\mathsf{negl}(n)$.
我们以后需要用到可忽略小的函数是, 不再显式地说出函数的名字, 而是直接用$\mathsf{negl}(\cdot)$表示. 这个记号类似于渐进记号, 如$O(n^3)$, 可以表示任何一个增长比$n^3$快的函数.