容错学习(learning with errors, LWE)问题就是求解带噪声的线性方程组问题, 由Oded Regev在[Reg05] 中提出, 他也因此结果荣获2018年的哥德尔奖. LWE问题的困难性基于的复杂性假设非常弱, 但是功能却异常强大, 由于LWE问题尚无有效的量子求解算法, 因此基于LWE假设的加密方案被认为是抗量子的.
LWE问题是求解带噪声的线性方程组问题. LWE问题的困难性基于的复杂性假设非常弱, 但是功能却异常强大, 由于LWE问题尚无有效的量子求解算法, 因此基于LWE假设的加密方案被认为是抗量子的.
终于到了介绍LWE的时间. LWE几乎是每个当代密码学学者\学生必须要有所了解的工具, 基于LWE, 我们能够构造一大批功能强大且安全的加密方案, 如选择密钥攻击安全的公钥加密方案(IND-CCA2 PKE), 有损加密方案(Lossy PKE), 基于属性加密(ABE), 全同态加密(FHE), 密钥交换(Key Exchange), 非交互零知识证明(NIZK), 程序混淆(Obfuscation)….
本文中, 我们将介绍LWE相关知识, 包括Basic Idea, 两种基本问题和他们之间的规约, 变体问题及其困难性规约, LWE算法的复杂性结论.
解线性方程组问题
没有什么可以说的呀, 求兼容的线性方程组的特解或者通解都是$\mathbf P$问题. 我们说的方程之间不兼容, 实际上是就是以下一种情况:
- 没有几个相互矛盾的方程, 比如一会儿又让$x_1+x_2=1$, 一会儿又让$x_1+x_2=2$.
但是产生这种情况的情形, 可能是多种的:
- 消元消除了$c=0$, 其中$c$是一个非零常数
- 两个方程系数有公约数, 模出来之后左边相同了右边又不同
不过, 大体上对于一个随机的$m$元$n$个方程组成的模$q$方程组, 只要参数得当(比如不要作死选$m<n$), 得到的方程几乎是可以解的. 一种比较好的方式的, 首先编造出来方程的解, 再来随机生成系数得到方程, 这样生成的方程组始终是有解的. 无论是哪种方式, 我们要解决的问题都是求线性方程组的解. 求解下列方程是容易的:
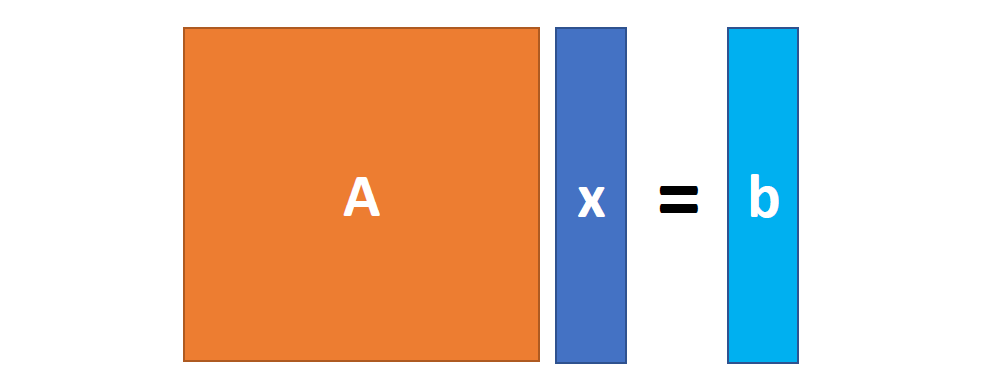
为了保持LWE问题研究的传统, 我们用$\mathbf s$来表示方程的解, 并称其为秘密向量. 这个问题是这样的, 首先, 挑战者(challenger)会均匀随机地选择一个$n$维的$\mathbf s$作为解. 我们作为攻击者(adversary)可以不断地向挑战者索要方程地组中的一个方程. 实际上, 此时挑战者在先前并没有准备方程, 此时挑战者会均匀随机的选择行向量$\mathbf a_i$作为方程的系数, 然后计算$b_i=\mathbf a_i\cdot \mathbf s$, 并将$(\mathbf a_i,b_i)$返回给攻击者. 攻击者在拿到一定数量($m$个)的方程后可以构建方程组$\mathbf A\mathbf s=\mathbf b$, 可以很有把握地输出方程地解$\mathbf x$. 这里的$\mathbf A$就是方程的系数矩阵即$\mathbf A$的每一行就是由$\mathbf a_1,\cdots, \mathbf a_m$构成. 实际上, 我们知道我们只要拿到$n$个线性无关$\mathbf a_i$构成的方程就可以成功解出$\mathbf x$.
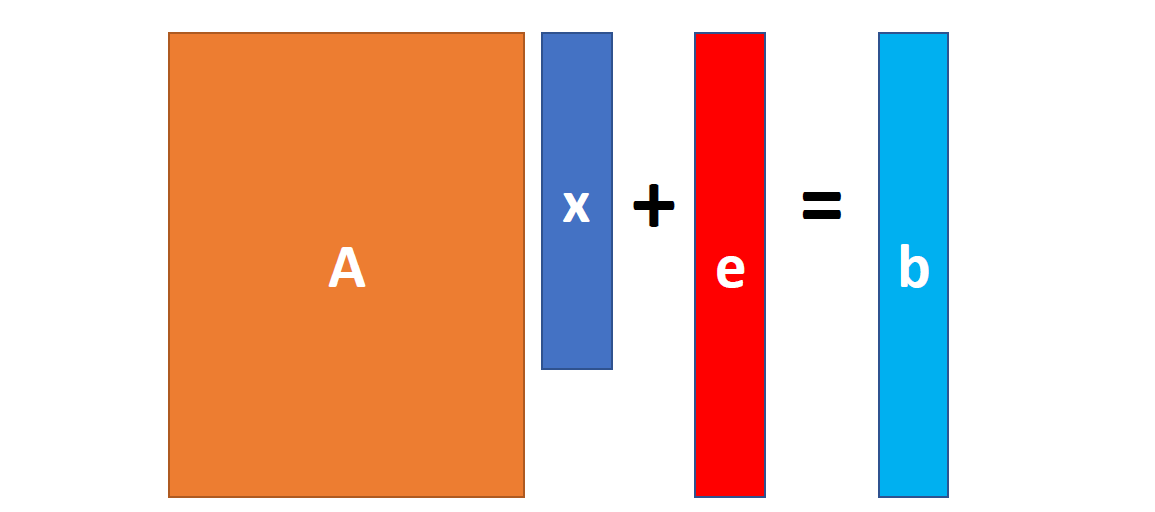
如果我们将问题变得复杂一些呢? 此时攻击者不会直接给我们$(\mathbf a_i,b_i=\mathbf a_i\cdot \mathbf s)$, 而是会在此基础上加一些料, 给$b_i$一些扰动$(\mathbf a_i,b_i=\mathbf a_i\cdot \mathbf s+e_i)$, 其中$e_i$服从一个均值为0, 方程较小的错误分布. 此时求解问题变成了求解这样的方程的解$\mathbf x$.
有两种极端的情况, 这两种情况是神仙也不能处理的:
- 方程数量过少, 只有小于或等于$n$个方程.
- 错误过大, 例如错误是均与随机的.
对于第一种情况, 我们如果按照线性方程组进行求解, 最好的情况也就是求出$\mathbf A\mathbf s=\mathbf e+\mathbf b$唯一的特解, 由于我们不知道除了$\mathbf e$的分布外有关它的任何信息, 根据这个信息来猜$\mathbf x$, 结果不会太好. 例如, 如果$\mathbf e$的每一行都是离散高斯分布, 且取到$0$的概率是$C$, 由于$e_i$取$0$的概率最大, 因此我们最佳的策略就是猜所有的$e_i=0$, 在这样最优的策略下, 我们正确解出$\mathbf x$的概率是$C^n$, 这是一个$\mathsf{negl}(n)$的概率.
对于第二种情况, 另一种情况, 我们相当于拿到的$(\mathbf a_i,b_i)$中的$b_i$永远是均匀的, 与$\mathbf s$一点关系都没有, 又由于$\mathbf a_i$也是挑战者均匀选取的, 因此攻击者拿到的永远是均匀随机的$(\mathbf a_i,b_i)$, 也就与$\mathbf x$无关的信息, 也就不可能能够求解出$\mathbf s$.
我在这里是不太想要讲解如何来解决这个问题的, 因为这里直接解释这个问题的Naive解法没有任何意义, 它需要用到BitDecomp的原理将方程$\mathbf{a}_i\cdot \mathbf s+e_i=b_i$转化为$\mathsf{Powerof2}(\mathbf a_i)\cdot \mathsf{BitDecomp}(\mathbf s)+e_i=b_i$后再做处理. 在学习完同态加密中BV11b方案后, 希望读者可以自行构造出naive的解法. 因此, 我将上述问题的naive算法作为了习题放在了介绍BV11b方案的文章中.
LWE问题
有了上述基础, 现在我们可以介绍LWE问题. 最基本的LWE问题有着两个版本, 这两个版本分别对应计算复杂性中两类最基本的问题, 且两个问题之间存在多项式时间的归约. 我们将分别介绍两个版本的LWE问题, 再介绍它们之间的归约方法.
在介绍两类问题之前, 我们首先介绍一些基础知识. 首先是LWE分布.
LWE分布
给定某个$\bf s\in \mathbb Z_q^n$和错误分布$\chi$, 定义LWE分布$A_{\mathbf s,\chi}$为: 均匀选择$\mathbf a\leftarrow \mathbb Z_q^n$并采样$e\leftarrow \chi$ ,计算$b=\mathbf a\cdot \mathbf s+e$并输出$(\mathbf a,b)$.
这里$\mathbf s$也就是秘密向量, 称$\chi$为噪声(或错误)分布, 称$e$为噪声(或错误). 我们可以理解为, 每次从LWE分布$A_{\mathbf s,\chi}$中采样, 都可以得到一个近似解为$\mathbf s$的线性方程. 如果有一个专门提供这样的分布的Oracle, 那么我们就可以多次来调用该Oracle已积攒足够数量的方程来求解该问题. 应该注意到, $A_{\mathbf s,\chi}$中我们省略了参数$n$, 这是一种常用的写法, 因为这里的$n$可以根据上下文推出. 我们牺牲部分符号上的严谨性来与大多数论文统一符号, 来帮助读者快速熟悉这些记号.
搜索LWE问题
搜索LWE问题(search LWE problem, SLWE)就是我们前边提到的解近似线性方程组的问题, 即
搜索LWE问题
SLWE$_{n,q,\chi,m}$问题定义为: 给出$A_{\mathbf s,\chi}$的Oracle, 在最多进行$m$次Oracle访问的情况下求$\mathbf s$.
该问题的表述可以是多种多样的, 有的表述中, 直接将$m$个Oracle的结果一并给出, 即均匀选择$\mathbf A\in\Z_q^{m\times n}$和采样$\mathbf e\leftarrow\chi^m$, 计算$\mathbf b=\mathbf {As}+\mathbf e$, 根据$(\mathbf A,\mathbf b)$求$\mathbf s$.
一般来说, 我们会要求$m$是一个有关于$n$的多项式, 即$m=m(n)$是一个多项式函数. 毕竟, 对于一个只能在概率多项式时间内运行的攻击者是无法有充足的时间访问超多项式次Oracle的.
判定LWE问题
判定LWE问题同其他判定一样, 要求输出的是YES/NO(或1/0).
判定LWE问题
DLWE$_{n,q,\chi,m}$问题定义为: 给出$m$个来自一下两个分布中的任何一个的采样结果:
- $A_{\mathbf s,\chi}$分布
- $\mathbb Z_q^n\times \mathbb Z_q$上的均匀分布
求采样结果所服从的分布.
下文中, 我们统一输出结果的方式: 如果拿到的是$A_{\mathbf s,\chi}$分布, 输出$1$为正确答案.
如果两个版本的LWE问题要求$m$均为多项式, 这个问题似乎这个问题看起来更加简单一些? 但是接下来我们将会发现, 这两个问题相互之间是可以概率多项式规约的, 即一台概率图灵机, 如果有求解两个问题中任何一个的Oracle的访问权限, 就可以在多项式时间内以压倒性概率求解另一个问题.
两个LWE问题之间的规约
我们用$\mathcal O_D$来表示与上下文相关的DLWE问题的求解器, 用$\mathcal O_S$来表示与上下文相关的SLWE的求解器. 这里参数$m=m(n)$是有个有关$n$的多项式函数.
DLWE$_{n,q,\chi,m}$ $\leq_\mathbf{BPP}$ SLWE$_{n,q,\chi,m}$
在拿到DLWE$_{n,q,\chi,m}$的实例$(\bf A, \bf b)$之后, 我们调用SLWE$_{n,q,\chi,m}$的Oracle, 然后得到$\mathbf s=\mathcal O_S(\mathbf A,\mathbf b)$, 然后检验$\mathbf e=\mathbf A\mathbf s-\mathbf b$是否服从$\chi^m$分布, 如果检验通过则输出$1$, 否则输出$0$.
我们非形式化地分析一下这个归约, 形式化的证明请读者自行完成. 假设我们拿到确实是LWE随机分布的随机变量, 这一随机变量交给SLWE的Oracle后我们的确能以非可忽略小的概率拿到$\mathbf s$, 重复多次后我们输出$1$的概率也就是压倒性[1]的. 此处忽略了一些细节, 例如假设检验也有可能出错, 但是这些都是在我们能够处理的范围内.
现在假设我们拿到的是非LWE分布的随机变量$(\mathbf A,\mathbf b)$, 该随机变量只有可忽略小的概率是可以表示成LWE分布, 因此$\mathbf s= \mathcal O_S(\mathbf A,\mathbf b)$能够使得$\mathbf e=\mathbf {As}-\mathbf b$通过假设检验的概率是可忽略小的, 因此我们重复多项式次后也只能以可忽略小的概率输出$1$.
SLWE$_{n,q,\chi,m}$ $\leq_\mathbf{BPP}$ DLWE$_{n,q,\chi,m}$
首先是对于$q$是素数的情况. 假设我们得到了SLWE$_{n,q,χ,m}$的实例$(\mathbf{A},\mathbf b)$, 假设最终正确的结果是$\mathbf s$, 我们来看如何用$\mathcal O_D$判断ss的第一位$s_1$是否为$k$.
首先, 均匀选择$\mathbf r^n\leftarrow\mathbb Z_q$, 再将$\mathbf A$的第一列加上$\mathbf r$得$\mathbf A’$, 并调用Oracle得到$d=\mathcal O_D(\mathbf A’,\mathbf b+k\cdot \mathbf r)$. 显然, 如果$s_1=k$, 那么$d=\mathcal O_D(\mathbf A’,\mathbf b+k\cdot \mathbf r)$就仍然是一个LWE的实例, 因为$\mathbf A’\mathbf s=\mathbf A\mathbf s+s_1\cdot \mathbf r=\mathbf b+k\cdot\mathbf r$, 其中$\mathbf r$为每个元素均为$r$的列向量. 如果$s_1=$的话, 那么$\mathbf A’\mathbf s+\mathbf e=\mathbf A\mathbf s+\mathbf e=\mathbf b$. 如果$s_1\neq k$, 则将会是均匀分布. 显然如果$\mathcal O_D$是一个靠谱的Oracle (即具有多项式分之一的区分优势), 那么我们重复以上过程多次, 将会以压倒性的概率正确判定$s_1$是否为$0$.
如果$q=\text{poly}(n)$, 那么经过多项式次上述测试, 就可以压倒性的概率求出$s_1$的值, 类似的可以依次求出$\mathbf s$的其他分量.
超多项式的$q$
如果是指数大小的$q$, 上述方法就不是特别管用了. 更好的办法就是用我们提到过的办法将方程$\mathbf{a}_i\cdot \mathbf s+e_i=b_i$转化为$\mathsf{Powerof2}(\mathbf a_i)\cdot \mathsf{BitDecomp}(\mathbf s)+e_i=b_i$后再做处理, 如果$q$是一个奇素数, 那么转换后的实例将也是LWE的实例, 且秘密向量都是$\mathsf{BitDecomp}(\mathbf s)\in\{0,1\}^{n\log q}$. 这样一来就不是紧归约了, 但是对于对于$q=2^{\text{poly}(n)}$来说, 我们仍有SLWE$_{n,q,\chi,m}\leq_\mathbf{BPP}$DLW$_{n\log q,q,\chi,m’}$, 其中$m’=\text{poly}(n)$.
LWE问题的复杂性结论
最坏情况下的复杂性结论
首先介绍在[Reg05]中最经典的结论.
定理[Reg05]
对于任意$m=\text{poly}(n)$, 任意$q\leq 2^{\text{poly}(n)}$和任意的高斯分布$\chi$满足$\alpha q\geq 2\sqrt n$, 其中$0<\alpha<1$, 如果存在一个高效求解DLWE$_{n,q,\chi,m}$的算法, 则存在一个高效求解$n$维格上满足参数$\gamma=\tilde O(n/\alpha)$的GapSVP$_\gamma$和SIVP$_\gamma$的量子算法.
这里的$\alpha q$就是高斯分布的标准差. 该结论也就是所, 如果有高效算法能够解决满足以上参数的DLWE问题, 也就存在一个量子算法能够解决相应的参数的GapSVP问题和SIVP问题. 这里的高效算法指的是$\mathbf{BQP}$算法. 能够归约到的GapSVP问题和SIVP问题的复杂度与参数$\alpha q$的选择有关, 如果选择$\alpha q=2\sqrt n$, 那么得能够归约上的GapSVP问题将会是$\mathbf{NP}\cap \mathbf {coNP}$的, 不太可能是一个$\mathbf{NP}$完备问题.
以上结论有用吗? 在GapSVP和SIVP有关的量子计算下的复杂性结论得出之前, 上述结论不能直接告诉我们什么. Chris Peikert与2009年在[Per09]中将上述结论经典化, 但参数会差一些:
定理[Pei09]
对于任意$m=\text{poly}(n)$, 任意$q\geq 2^{n/2}$和任意的高斯分布$\chi$满足$\alpha q\geq 2\sqrt n$, 其中$0<\alpha<1$, 如果存在一个高效求解DLWE$_{n,q,\chi,m}$的算法, 则存在一个高效求解$n$维格上满足参数$\gamma=\tilde O(n/\alpha)$的GapSVP$_\gamma$的算法.
由于整个归约是纯经典的, 因此如果求解DLWE的高效算法是经典的, 那么得到的结论中, 高效求解GapSVP算法也就是经典的.
平均情况下的复杂性结论
其他版本的LWE问题
错误分布与噪声分布相同
在BGV12同态加密方案中, 我们为了使得密钥$\mathbf s$的$\ell_1$较小哦啊, 而选择从噪声分布中选取$\mathbf s$. 这里的安全性是有理论依据的. 在[ACPS09]中, 我们有如下结论:
定理[ACPS09]
其他信息
- 有关Worst-case Hardness与Average-case Hardness的概念及讨论, 可以参考文章Levin’s Theorem, 当这篇文章写成后, 地址将被更新到这里.
论文索引
[ACPS09] B. Applebaum, D. Cash, C. Peikert, and A. Sahai. Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In CRYPTO, pages 595-618. 2009.
[Pei09]
[Reg05] On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. J. ACM, 56(6):1-40, 2009. Preliminary version in STOC 2005.
注释
- 1.翻译自英文overwhelming, 一个压倒性的函数即满足$\mathsf{overwhelm}(n)=1-\mathsf{negl}(n)$的函数. ↩